细粉加工设备(20-400目)

我公司自主研发的MTW欧版磨、LM立式磨等细粉加工设备，拥有多项国家专利，能够将石灰石、方解石、碳酸钙、重晶石、石膏、膨润土等物料研磨至20-400目，是您在电厂脱硫、煤粉制备、重钙加工等工业制粉领域的得力助手。

MTW系列欧版磨粉机

稀油润滑系统，新型吊挂式笼式选粉机结构设计

LM立式辊磨机

采用新型碾磨装置自动化电控系统

5X系列欧版智能磨粉机

大型规模化环保智能磨粉机优选设备

LM矿渣立式磨

LM矿渣立式磨集破碎、干燥、粉磨、分级输送于一体

立式磨煤机

烘干与制粉二合一可边磨边烘干

雷蒙磨粉机

工业磨粉设备先驱，经济实用

更多了解

超细粉加工设备(400-3250目)

LUM超细立磨、MW环辊微粉磨吸收现代工业磨粉技术，专注于400-3250目范围内超细粉磨加工，细度可调可控，突破超细粉加工产能瓶颈，是超细粉加工领域粉磨装备的良好选择。

LUM超细立磨

LUM超细立磨结合现代磨粉理念

MW环辊微粉磨

采用新型碾磨装置自动化电控系统

粗粉加工设备(0-3MM)

兼具磨粉机和破碎机性能优势，产量高、破碎比大、成品率高，在粗粉加工方面成绩斐然。

LM砂粉立磨

大型效率与节能双高型砂粉制备产品

f分别是bcf分别是bcf分别是bc

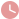
(1)如图1,正方形ABCD中,E、F分别是BC、CD边上的点,且

(1)如图1,正方形ABCD中,E、F分别是BC、CD边上的点,且满足BE=CF,连接AE、BF交于点H请直接写出线段AE与BF的数量关系和位置关系 (2)如图2,在正(1)如图①，在正方形 ABCD 中，点 E,F 分别是边 BC,CD 上的点， BE=CF, AF,DE 交于点 G 求证： AF⊥DE 且 AF=DE (2)点 E,F 分别在边 CB,DC 的延长线上，且 BE=CF (1)中 (1)如图①，在正方形 ABCD 中，点 E,F 分别是边 BC,CD 上

如图，正方形ABCD中，E、F分别是BC、CD的中点，AE

2011年9月23日 20210222 回答 ∵ABCD是正方形 ∴角又：E、F分别是BC、CD的中点 ∴BE=CF 在三角形ABE与 BCF中，AB=BC，角ABE=角BCF，BE=CF ∴ ABE ≌ BCF 如右图，四边形 ABCD 是边长为 1 的正方形， E 、 F 分别是 BC 、 CD 的中点．阴影部分面积是．相关知识点：空间与几何平面图形封闭图形直线型三角形三角形的面积直线如右图，四边形ABCD是边长为1的正方形，E、F分别是BC

又∵E，F分别是边AB．BC的中点 zuoyebang

答案解析查看更多优质解析解答一举报证明：（1）∵四边形ABCD为正方形 ∴AB=BC=CD=AD，∠ABF=∠DAE=90°，又∵E，F分别是边AB．BC的中点 ∴ AE＝ 18如图，矩形ABCD中，点E在边CD上，将 BCE沿BE折叠，点C落在AD边上的点F处，过点F作FG∥CD交BE于点G，连接CG (1)求证：四边形CEFG是菱形； (2) 八年级数学下册《图形的折叠问题》练习题与答案 (人教版)

如图，已知正方形ABCD的边长为3，E、F分别是AB、BC边

如图，已知正方形ABCD的边长为3，E、F分别是AB、BC边上的点，且∠EDF=45^ {\circ}，将\triangle DAE绕点D按逆时针方向旋转90^ {\circ}得到\triangle DCM． (1)求证：EF=MF； 2024年3月9日 4、如图，PC切圆O于C，AC为圆的直径，PEF为圆的割线，AE、AF与直线PO相交于B、D．求证：AB＝DC，BC＝AD． 4、平行四边形ABCD中，设E、F分别中考数学 20道你不得不会做的经典几何难题正方形四边形

【废水处理问答】什么叫B/C? B/C有什么意义?

2017年11月19日 B C是BOD与COD比值的缩写，该比值可以表示废水中可生化降解特性。当比值≥0 45时，表示不可生物降解的有机物占全部有机物的20%以下，而当比值≤0 2 如图等腰梯形ABCD中AD∥BCMN分别是ADBC的中点EF分别是BMCM中点． (1)求证:四边形MENF是菱形, (2)若四边形MENF是正方形请探索等腰梯形ABCD的高和底边BC的数量关系并证明你的结论．如图等腰梯形ABCD中AD∥BCMN分别是ADBC的中点E

如图，在 ABC中，∠ ACB=90°，AC=BC，点D是线段BC边

如图，在 ABC中，∠ ACB=90°，AC=BC，点D是线段BC边上的一点，连结AD，点E在射线BC上，过E作EF⊥ AD交AD于点F (1)如图1，当D是BC的中点，且DF=BD时，若AB=4√2，求CE的长； (2)如图2，当CE=CD时，延长EF交AB于点G，取AD的中点H，连结EH，过点A作AM ∥ BE，交EH的延长线于点M，猜想AM与BG之间的数量关系并证明1 2 DM＝DC ．（1）正方形ABCD中，AB=BC，BF=AE，且∠ABF=∠DAE=90°，即可证明 ABF≌ DAE，即可得∠DGA=90°，结论成立．（2）延长AF交DC延长线于M，证明 ABF≌ MCF，说明 DGM是直角三角形，命题得证．本题考点：全等三角形的判定与性质；直角三角形的性质；正方形的又∵E，F分别是边AB．BC的中点 zuoyebang

如图，在正方形ABCD中，E、F分别是BC、DC上的两点

解析（1）∵四边形ABCD是正方形， ∴AB=AD=CD；∠ADC=∠B=90° ∴将 ABE逆时针旋转90°至 ADM，如图1所示 ∴ ABE≌ ADM ∴AM=AE；BE=DM；∠ADM=∠B=90°；∠DAM=∠BAE ∴∠ADM+∠ADC=180° ∴C、D、M在同一直线上 ∴EF=DF+BE=DF+DM=MF，在 AEF和如图，在 ABC中，BD，CE分别是边AC，AB上的中线，BD与CE相交于点O（1）BO与OD的长度有什么关系？（提示：分别作BO，CO的中点M，N，连接ED，EM，百度教育结果1 结果2如图，在 ABC中，BD，CE分别是边AC，AB上的中线，BD

如图，在正方形ABCD中，点E、F分别是BC、DC边上的两点

2015年2月9日如图，在正方形ABCD中，点E、F分别是BC、DC边上的两点，且∠EAF=45°，AE、AF分别交BD于M、N．下列结论：答：长方形的面积是60平方厘米．故答案为：60．先证明DG是GE的两倍，可用面积证明：连接AG，因为E，F分别是AB，DA的中点，三角形AEG、三角形BEG、三角形AGF、三角形FGD的面积都相等，所以三角形ADG的面积：三角形AGE的面积=2：1，即DG：GE=2：1，所以三角形DCG的如图中，ABCD是长方形，E，F分别是AB，DA的中点，G

如图,在菱形ABCD中,E、F分别是BC、CD上的点,且CE=CF

(2) 若∠B=60°,点E、F分别为BC和CD的中点求证: AEF为等边三角形 B E 相关知识点：四边形特殊的平行四边形菱形菱形的性质菱形的性质——与边相关菱形的性质——与角相关菱形的性质——与对角线相关菱形性质综合应用试题来源：2012年5月3日正方形ABCD中,E,F分别是BC,CD的中点,AE,BF交于点P 求证:AD=PD证明：取AB的中点G，连接DG，交AE于H∵四边形ABCD是正方形∴AB=BC=CD，∠ABE=∠BCF=90º∵E,F分别是BC,CD的中点∴BE=CF∴⊿ABE≌⊿BCF（SAS）∴∠BAE正方形ABCD中,E,F分别是BC,CD的中点,AE,BF交于点P

已知，菱形ABCD中，点E，F分别是BC，CD上的点，且AE

分析：首先根据菱形的性质和已知条件可证明 ABE≌ ADF，所以∠BAE=∠DAF，再根据三角形的内角和为180°，可求出∠C的度数，进而求出∠B的度数．2015年1月10日举报（1）如图1，正方形ABCD中，E、F分别是BC、CD边上的点，且满足BE=CF，连接AE、BF交于点H请直接写出线段（1）解：AE=BF且AE⊥BF，理由是：∵四边形ABCD是正方形，∴∠ABE=∠C=90°，AB=BC，∵在 ABE和 BCF中AB＝B（1）如图1，正方形ABCD中，E、F分别是BC、CD边上的

在正方形ABCD中，E、F分别是CD、AD的中点，AE、BF

2012年5月21日在正方形ABCD中，E、F分别是CD、AD的中点，AE、BF相交于P，求证：CP=CB如图，G是AB中点，连接CG，交FB于Q先证三角形ADE和BAF全等（直角、正方形边长、边长一半）再证AE垂直BF（角1+角2=90度，角1=角1'，角1'2016年11月25日如图，点D，E分别是 ABC的边AC，AB上的点，直线BD与CE交于点F，已知 CDF， BFE， BCF的面积分别是3，如图，连接AF，，∵ CDF， BFE， BCF的面积分别是3，4，5，∴S ABFS ADF=BFDF，S BFCS CDF=BFDF=53，S如图，点D，E分别是 ABC的边AC，AB上的点，直线BD与

如图，已知菱形ABCD，AB=AC，E、F分别是BC、AD的

3 ．（1）根据菱形的四条边都相等可得AB=BC，然后判断出 ABC是等边三角形，然后根据等腰三角形三线合一的性质可得AE⊥BC，∠AEC=90°，再根据菱形的对边平行且相等以及中点的定义求出AF与EC平行且相等，从而判定出四边形AECF是平行四边形，再根据有一个角是直角的平行四边形是矩形即可得证；答案欲求AE•CF，先把要求数量积的两个向量表示成以四面体的棱所在向量为基底的向量的表示形式，写出向量的数量积，问题转化成四面体的棱向量之间的关系，因为棱长及其夹角可知，从而得到结果．在棱长为2的正四面体ABCD中,E,F分别是BC,AD的中点,则在棱长为2的正四面体ABCD中,E,F分别是BC,AD的中点,则

如右图，四边形ABCD是边长为1的正方形，E、F分别是BC

如右图，四边形 ABCD 是边长为 1 的正方形， E 、 F 分别是 BC 、 CD 的中点．阴影部分面积是．相关知识点：空间与几何平面图形封闭图形直线型三角形三角形的面积直线型曲线型综合题型阴影部分的周长和面积试题来源：如图，在 ABC中，∠BAC=90°，AB=AC=6，D为BC的中点．（1）若E、F分别是AB、AC上的点，且AE=CF，求证： AED≌ CFD；（2）当点F、E分别从C、A两点同时出发，以每秒1个单位长度的速度沿CA、AB运动，到点A、B时停止；设 DEF的面积为y，F点运动的时间为x，求y与x的函数关系式；（3）在（2）的条件下，点F、E 如图，在 ABC中，∠BAC=90°，AB=AC=6，D为BC的中点

如图，在梯形ABCD中，AD∥BC,点E,F分别是AD,BC的中点

相关知识点：试题来源：解析证明：过点E作AB、CD的平行线，与BC分别交于G，H，可得∠EGH=∠B，∠EHG=∠C， ∵∠B+∠C=90 2013年10月9日 A是三角形BCD所在平面外的一点，E，F分别是BC，AD的中点 1)求证EF于BD是异面直线 2）若AC垂直BD，AC=BD,求EF与BD所成的角分享 A是三角形BCD所在平面外的一点，E，F分别是BC，AD的

如图： ABC中，AB=BC，D、E、F分别是BC、AC、AB边

2012年3月15日如图： ABC中，AB=BC，D、E、F分别是BC、AC、AB边上的中点。〈1〉求证：四边形BDEF是菱形：〈2〉1证明：∵D、E、F分别是BC、AC、AB边上的中点∴DE，EF都是⊿ABC的中位线∴DE=½AB=BF EF=½BC=BD∵AB=BC如图等腰梯形ABCD中AD∥BCMN分别是ADBC的中点EF分别是BMCM中点． (1)求证:四边形MENF是菱形, (2)若四边形MENF是正方形请探索等腰梯形ABCD的高和底边BC的数量关系并证明你的结论．如图等腰梯形ABCD中AD∥BCMN分别是ADBC的中点E

如图，在 ABC中，∠ ACB=90°，AC=BC，点D是线段BC边

如图，在正方形ABCD中，E、F分别是BC、DC上的两点

如图，在正方形ABCD中，点E、F分别是BC、DC边上的两点

如图,在菱形ABCD中,E、F分别是BC、CD上的点,且CE=CF

(2) 若∠B=60°,点E、F分别为BC和CD的中点求证: AEF为等边三角形 B E 相关知识点：四边形特殊的平行四边形菱形菱形的性质菱形的性质——与边相关菱形的性质——与角相关菱形的性质——与对角线相关菱形性质综合应用试题来源：2012年5月3日 ABE与 BCF中，AB = BC，BE = CF，角ABC = 角BCD = 90°。因此 ABE≌ BCF。因此∠BAE = ∠CBF。又∠CBF+∠ABF = 90°，所以∠BAE+∠ABF = 90°。所以∠APB = 90°。由此得出BF⊥AE。正方形ABCD中,E,F分别是BC,CD的中点,AE,BF交于点P

已知，菱形ABCD中，点E，F分别是BC，CD上的点，且AE

分析：首先根据菱形的性质和已知条件可证明 ABE≌ ADF，所以∠BAE=∠DAF，再根据三角形的内角和为180°，可求出∠C的度数，进而求出∠B的度数．

空中打击筛分磨粉机

粉碎黄土机器

中小型选厂粉碎系统两段一闭路

2plf双齿辊磨粉机参数

每亿元投资需要氢氧化钙

出口磨粉机厂家

PE2501000立式磨粉机轴承型号

本机在正常工作状态下

博洛斯洛破壁机

时产120吨硅石岩石磨粉机

板式给料机

立磨护板

蒸汽块砖生产视频

制粉机稀油站用油管

松滋云安矿山机械

立式辊磨机产量60TH

沙石设备

工业废渣对环境的危害

脱碳煤矸石磨粉机械多少

立式研磨粉机

时产1800吨立式矿石磨粉机

磨粉机和研磨机

立式磨粉机使用说明书英

砂场承包方案视频

二手矿山设备对辊北京

滑石生产线厂家滑石生产线厂家滑石生产线厂家

矿粉厂办证手续有哪些

石墨磨具机械那里买

石子开采

榨汁机磨粉机区别